Distributed Self-Distillation

Self-distillation training involves a student model learning from a teacher model that is maintained as an exponential moving average (EMA) of the student's weights. When scaling this approach across multiple GPUs, the challenge lies in efficiently distributing both networks while respecting their different update mechanisms—the student trains via backpropagation, while the teacher updates through EMA. We examine three distributed training strategies: (1) replicating both models with DDP, which is simple but memory-intensive; (2) sharding only the student with FSDP; and (3) identically sharding both student and teacher with FSDP, making the teacher EMA update purely local with no communication overhead. The key insight is that effective distributed training must align with the algorithm's structure. In this case, identical sharding naturally respects the EMA dependency between networks.

Distillation & Self-Distillation

Knowledge distillation is a method where a student model learns from a teacher model, often by matching the teacher's outputs or intermediate representations. Traditionally, the teacher is a larger, pre-trained model, and the student is smaller and initialised randomly (although the student is not always smaller, see e.g. HuBERT). The goal of distillation is to transfer knowledge from the teacher into the student so the student can achieve similar performance with fewer parameters. Put very generally, the goal of distillation is for the student to achieve comparable performance as the teacher on some task using a smaller model.

We can refer to the setup above as Fixed Teacher Distillation. Self-distillation evolves this idea, with two key differences: (1) the teacher and student share the same architecture, and (2) there is no separate pre-trained teacher.

A conceptual middle ground between fixed and continuous teacher updates is HuBERT, which iteratively re-trains: the model generates pseudo-labels, then a new model is trained on those labels, which generates better pseudo-labels, and so on. Self-distillation takes this to its continuous limit—rather than discrete re-training rounds, the teacher is maintained as an Exponential Moving Average (EMA) of the student's weights, updated after every training iteration:

$\theta_{\text{teacher}}(t) = \tau \theta_{\text{teacher}}(t-1) + (1-\tau) \theta_{\text{student}}(t)$

where τ is a momentum coefficient (typically between 0.99 and 0.999).

The update dynamics are as follows:

• Student update: The student is trained with gradient descent, minimizing a loss that aligns its outputs with the teacher's outputs. This involves a backward pass through the student network.
• Teacher update: The teacher is never updated through backpropagation—it is only updated via EMA of the student, making it a lagged and smoothed version of the student. This update requires access to the student parameters.

The teacher is initialized by copying the initial student weights, but over time it acts as an implicit ensemble of past student models, making it more stable and less noisy than the current student. This provides richer, higher-quality targets, enabling the student to keep improving in an iterative bootstrapping loop.

One influential example of this approach is DINO, which trains Vision Transformers without labels by aligning the student's predictions to those of the EMA teacher across multiple augmented views of the same image.

Distributed Self-Distillation – Replicated Student and Teacher

When scaling self-distillation training across multiple GPUs, an important technical challenge arises: how to efficiently train both the student and the teacher models in a distributed fashion. Both networks need to process the same inputs and produce aligned outputs, but their update mechanisms differ. The student updates via gradient descent with backpropagation, while the teacher updates as an EMA of the student's parameters after each iteration. We focus only on data parallel techniques in this post. We won't duplicate work by others by describing different parallelisation techniques in detail. Instead, we'll just refer the reader to How To Scale Your Model and the HuggingFace Ultra-Scale Playbook, both of which are worth a read.

The most straightforward solution is to duplicate both the student and the teacher on every GPU, and train the student using Distributed Data Parallel (DDP). In this setup, each GPU holds a full copy of the student (with gradients and optimizer states) and a full copy of the teacher (updated via EMA of the student on that GPU). Training proceeds as follows:

Forward pass:

The whole batch is split into per-gpu minibatches. Each GPU then proceeds to compute the teacher and student forward passes for its corresponding minibatch. Each GPU then computes its own local loss, that is the loss between the teacher and student outputs wrt. the data that was processed on that GPU.

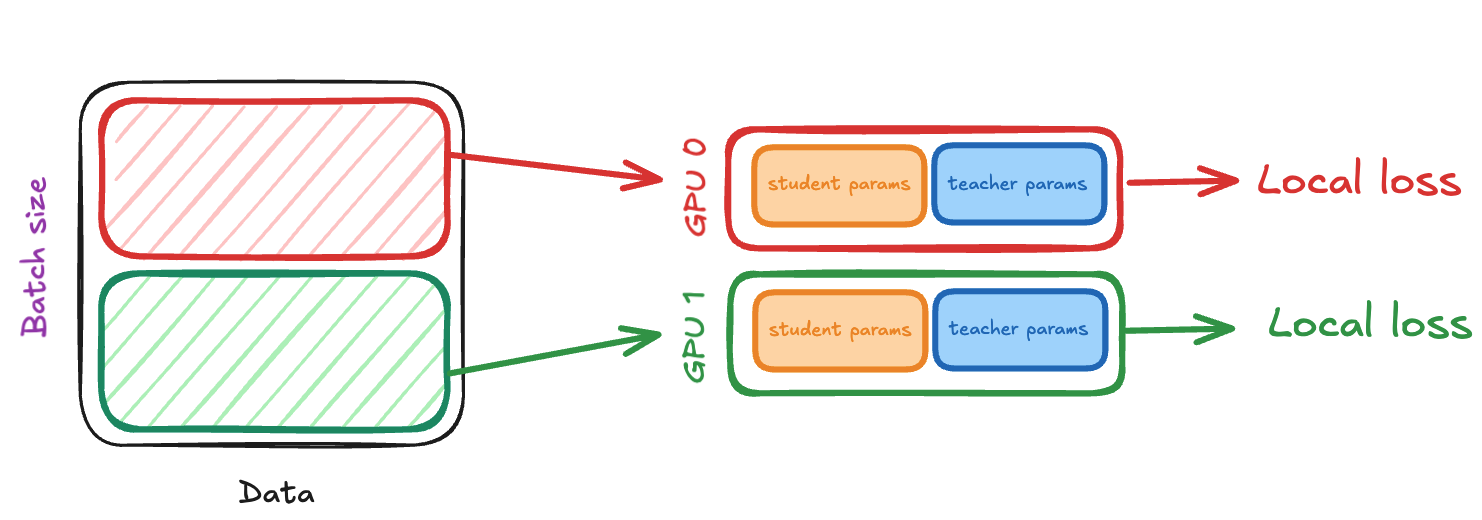
Update mechanism:

First the student network is updated. The student update involves first doing a local backward pass on the local loss to produce a "local gradient" for each GPU. An all-reduce is then performed on those gradients and applied to all copies of the student network across GPUs. This effectively results in us replicating the student parameter update across our GPUs. Once our student update is complete, we can then begin our teacher EMA update, which involves updating all copies of the teacher with the student stored on the same GPU.

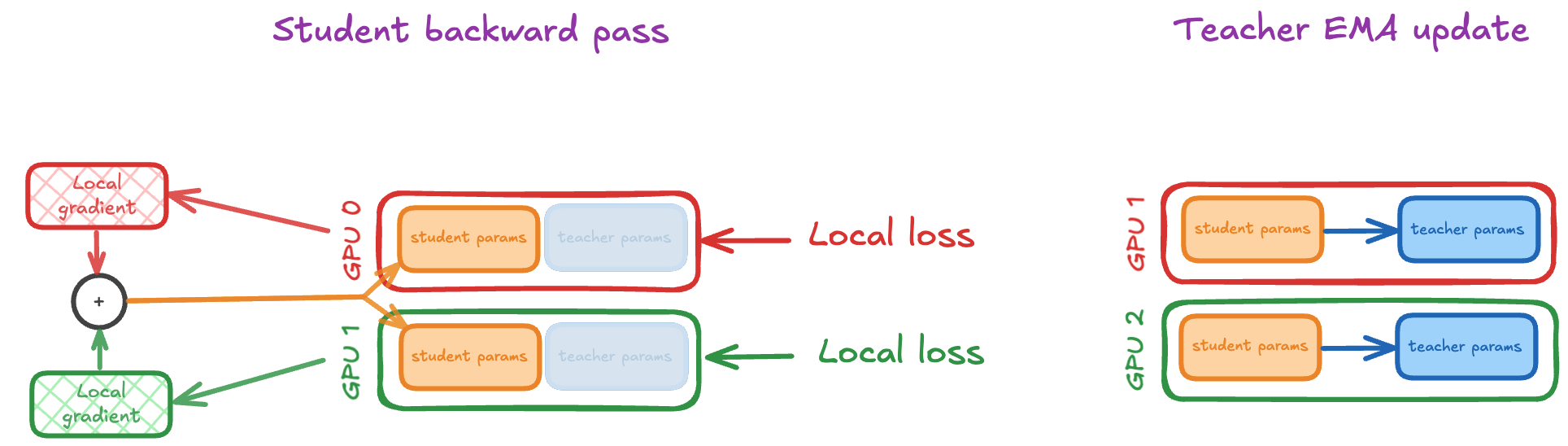
This is very simple to implement with standard DDP training code. No custom distributed communication or parameter sharding is required here. Now let's calculate our student and teacher models' GPU memory usage with this training setup (excluding activations). If we have P parameters in our student/teacher networks we can calculate that we end up storing 14P bytes per GPU:

Component	Memory
Student weights (BF16)	2P
Student gradients (BF16)	2P
Student Optimizer states (FP32) (Adam - 2 momentum states per parameter)	8P
Teacher weights (BF16)	2P
Total	14P

This is quite high. Depending on the model size and our GPU memory size, we may not be able to actually fit this in memory. We can do better. Notice that we also do some redundant computations: both the student gradient update and the teacher EMA updates are performed identically on all GPUs. The end result is that we keep multiple sets of identical weights for both student and teacher across different GPUs which we can definitely improve on.

FSDP Student with Replicated Teacher

The student consumes the majority of memory due to gradients and optimizer states. Of the 14P parameters, 12P are dedicated to the student. We can address this by sharding our student with Fully Sharded Data Parallel (FSDP/ZeRO-3 sharding). The teacher, requiring no gradients or optimizer states, remains fully replicated on every GPU.

Forward Pass:

The forward pass now proceeds similarly to before, except that since the student is sharded across our GPUs, we need to AllGather the relevant parameters during the student forward pass. Everything else remains the same.

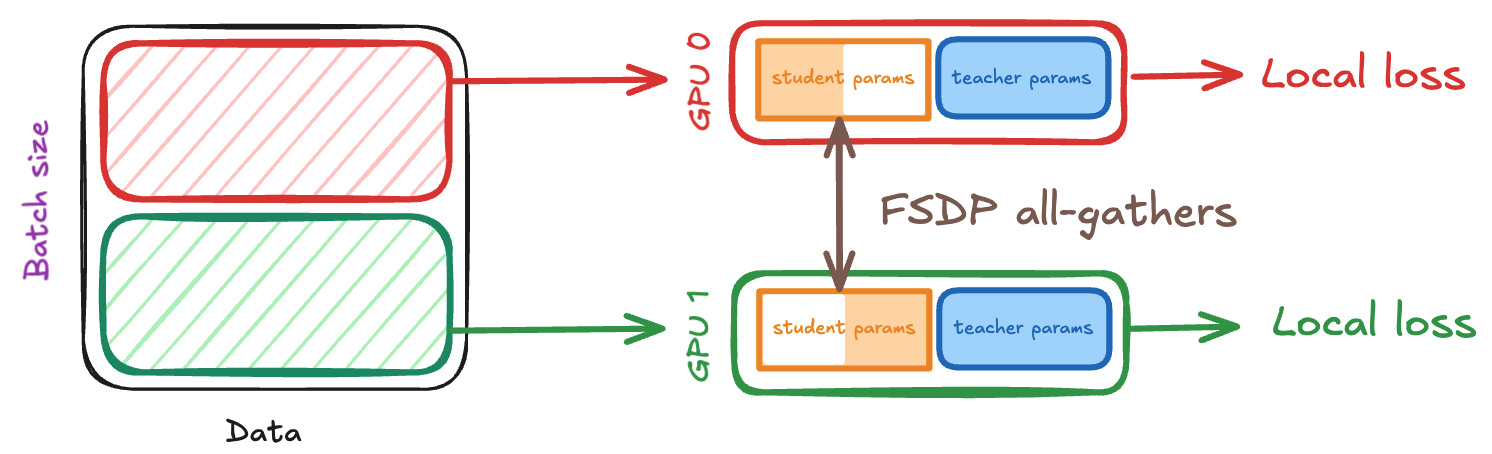
Update mechanism:

Similarly to the forward pass, we need to AllGather our student parameters during the student backward pass. Now, when we combine the local gradients, instead of applying an all-reduce operation, we apply a ReduceScatter, which effectively first performs an all-reduces and then reshards our gradient according to the way our student parameters are sharded. When it comes to the teacher EMA update, since the student parameters are sharded across the GPUs, we can't immediately update the teacher. First we need to AllGather the student to materialise a copy on each GPU, and only then can we continue to perform the identical teacher update on each GPU.

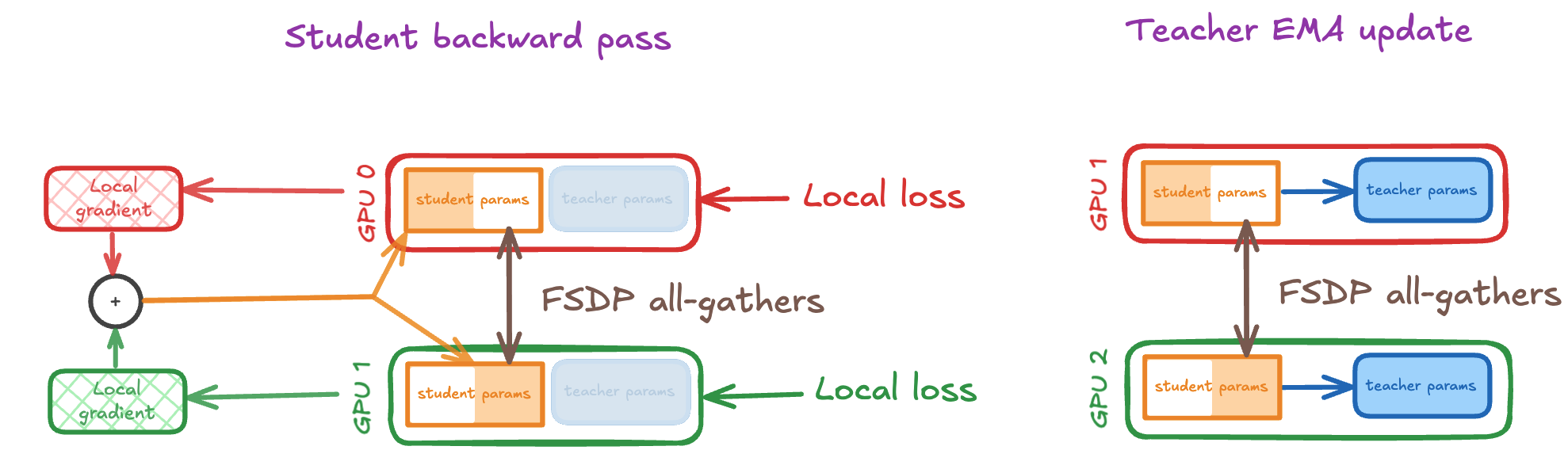
By wrapping the student in FSDP, we immediately save on the memory used. If we have N GPUs, then sharding the student reduces the memory used by the student by a factor of N, thus we get a total memory requirement of 14P/N + 2P = (14/N + 2)P. This is a lot better, and can help us train bigger models, and increase our batch size.

However, notice that while we have saved some GPU memory, we have introduced 3 AllGathers (student forward, student backward, teacher EMA update). In the case of the forward and backward passes, these can be overlapped with our big matmuls. However, we have no way of hiding the student AllGather in the teacher EMA update, as we are blocked by the student having completed its update before we begin AllGathering. So although we save on memory which can help us train larger models and increase our batch size, we will run into longer train step times.¹ How much this slows down our training is of course dependent on the model size and our bandwidth. For context, for H100s with NVLink interconnects (900GB/s), our AllGather will take 50ms for a model size of ~25B params.²

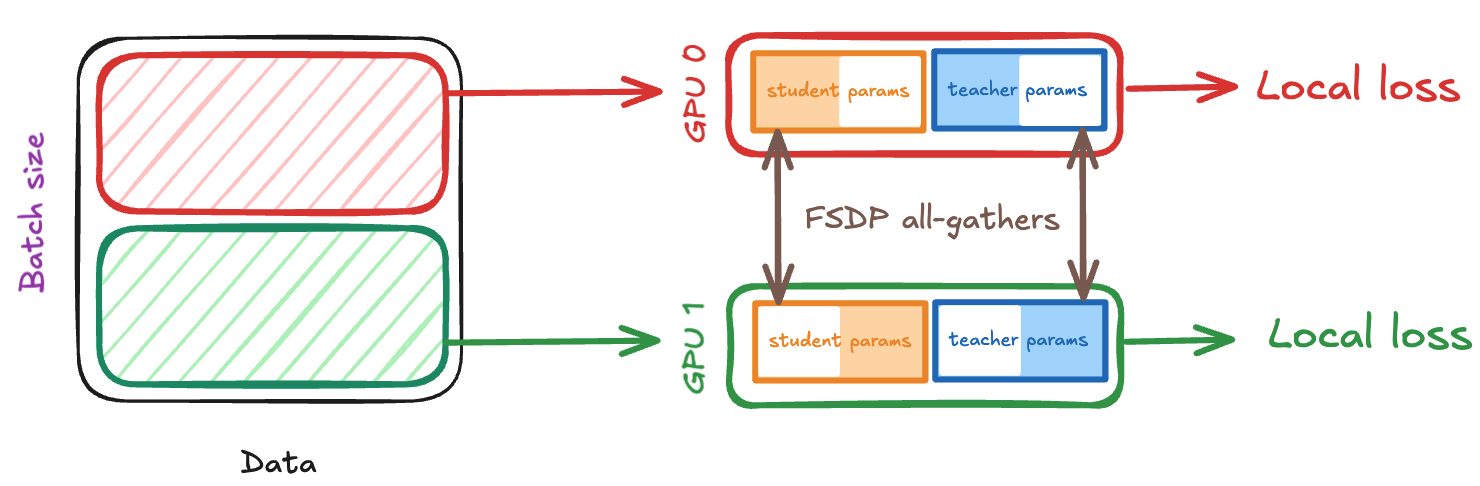
FSDP Student and Teacher with Identical Sharding

So far we have cut down significantly on the memory requirement by FSDPing the student, but now we've introduced a new AllGather which may cause our GPU utilisation to take a hit when training larger models, and we're also replicating identical EMA updates across each GPU, which is suboptimal. We can address both of these problems by sharding both the student and teacher identically with FSDP. By identically sharding, we essentially mean that each GPU will hold the exact same shard of both the student and teacher networks.

Forward Pass:

The forward pass looks quite similar to before, except that we also now need to AllGather the teacher parameters in the teacher forward pass, all of which can be hidden away behind forward pass computations.

Update mechanism:

While the student backward pass remains the same, the teacher EMA update now doesn't require an AllGather and has become entirely local, as each GPU is storing the same components or shards of both the student and teacher network. Our 2 networks are stored across multiple GPUs, but as far as each GPU is concerned, it has all of the relevant parameters to perform its own update. No AllGather required! Each GPU effectively completes its 1/N portion of the EMA update, and we avoid replicating any work.

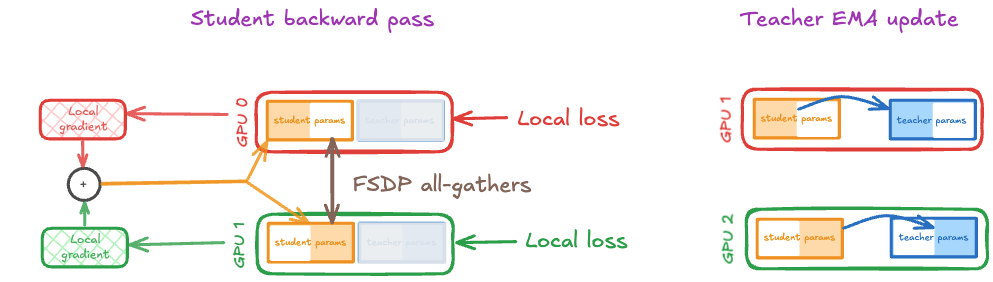
We have now gotten around having to do an extra AllGather operation, and simultaneously reduced the total work done in the EMA update by a factor of N. The reduction in total computations here is unlikely to matter much, if at all, as the teacher update is an elementwise operation that happens very quickly, and is communication bound by parameter loading bandwidth within a GPU, as opposed to the inter-gpu bandwidth that an AllGather depends on, which is approximately an order of magnitude slower. On the other hand, the removal of the AllGather can give a noticeable bump in GPU utilisation. A nice side effect is that we've also now slightly reduced our memory requirement down to 14P/N.

On a practical note, in order to identically shard our student and teacher models, we need to make sure that these have the exact same architecture. We can achieve this by initialising our teacher as a deepcopy of our student (or vice versa) eg. with teacher = copy.deepcopy(student). We then just wrap both models in FSDP via fsdp_model = FSDP(model, **fsdp_config). If we make sure to pass in the same fsdp_config, then PyTorch will deterministically shard these two different networks identically across our GPUs. In practice, the teacher EMA update is straightforward since each GPU only needs to access its local shards:

with torch.no_grad():
    for teacher_param, student_param in zip(teacher.parameters(), student.parameters()):
        teacher_param.data.mul_(tau).add_(student_param.data, alpha=1-tau)

Since both models are identically sharded, teacher_param and student_param on each GPU correspond to the same parameter shard, making this a purely local operation with no communication overhead.

Conclusion

We've explored three approaches to scaling self-distillation training across multiple GPUs, progressively optimizing both memory efficiency and training speed. Starting from the naive approach of replicating both models (14P per GPU), we moved to sharding only the student ((12/N + 2)P), which saved memory but introduced an unhideable AllGather that degraded iteration time. Our final approach—identically sharding both networks (14P/N)—achieves the best of both worlds: it reduces memory usage by a factor of N while eliminating the blocking AllGather, making the teacher update purely local and restoring full training speed.

While distributed training for a single network is relatively straightforward, the addition of multiple interacting networks—whether in self-distillation, reinforcement learning with policy and value networks, or other multi-model training paradigms—introduces a new dimension of complexity around how to arrange your computational topology. The lesson here is that effective distributed training setups must respect the underlying algorithm's structure. In our case, the EMA dependency between teacher and student makes identical sharding the natural choice, keeping parameter updates local. In other multi-network settings, such as RL where networks may have different update patterns or dependencies, alternative topologies that align with those algorithmic requirements may be more appropriate. The key is designing your distributed strategy around the algorithm, not forcing the algorithm into a standard distributed pattern.

---

1. Since we're really splitting hairs here, it's worth mentioning that part of the extra time spent on the AllGather will be compensated by the fact this set-up also results in a faster optimizer step when updating the student, due to each GPU only updating its portion of the sharded student network as opposed to the entire network. However, this won't fully make up for the extra time spent on the AllGather as the AllGather is bound by communication between GPUs, whereas the optimizer step is bound by communication within a GPU.↩
2. Another alternative to our teacher EMA update, is that we could gather our full student parameters only on rank 0 via the FSDP.summon_full_params(student_model, writeback=False, rank0_only=True) context manager, update the teacher on rank 0 only, and then broadcast a copy of the teacher from rank 0 to all other GPUs via for param in teacher_model.parameters(): dist.broadcast(param.data, src=0). This allows our GPUs to do less work overall and avoids replicating our teacher EMA update. However, gathering our student parameters onto 1 GPU will actually take the same amount of time as AllGathering student weights across all GPUs, we just end up with some of our bandwidth between GPUs being unused. The parameter elementwise update would take the same amount of time on one GPU as it would replicating this on all GPUs. We also end up having to spend extra time re-broadcasting our updated rank 0 teacher to other GPUs. We would end up with less bandwidth utilisation which could be useful if we actually had something to do with it. However, in this scenario we are simply left with longer time per iteration and is ultimately not worthwhile.↩